FORMAT OF THE GMAT MATH SECTION
The Math section consists of 21 multiple-choice questions and is 45 minutes long. The questions come in two formats: the standard multiple-choice question, which we will study in this section, and the Data Sufficiency question which we will study in the Data Insights section. The math section is designed to test your ability to solve problems, not to test your mathematical knowledge.
GMAT VS. SAT
GMAT math is similar to SAT math, though slightly harder. The mathematical skills tested are very basic: only first-year high school algebra and coordinate geometry. However, this does not mean that the math section is easy. The medium of basic mathematics is chosen so that everyone taking the test will be on a fairly even playing field. Although the questions require only basic mathematics and all have simple solutions, it can require considerable ingenuity to find the simple solution. If you have taken a course in calculus or another advanced math topic, don’t assume that you will find the math section easy. Other than increasing your mathematical maturity, little you learned in calculus will help on the GMAT.
As mentioned above, every GMAT math problem has a simple solution, but finding that simple solution may not be easy. The intent of the math section is to test how skilled you are at finding the simple solutions. The premise is that if you spend a lot of time working out long solutions you will not finish as much of the test as students who spot the short, simple solutions. So, if you find yourself performing long calculations or applying advanced mathematics—stop. You’re heading in the wrong direction.
Are you ready for the GMAT?
With our comprehensive book, you can be sure!
Although the GMAT is difficult, it is very learnable. GMAT Prep Course presents a thorough analysis of the GMAT and introduces numerous analytic techniques that will help you immensely, not only on the GMAT but in business school as well.

Nova’s GMAT Prep Course is the best GMAT prep book available, providing the equivalent of a 50-hour, 6-week course. This comprehensive test prep book provides twenty-two chapters of review material and hundreds of GMAT-style practice problems and examples. Plus, we’ll take you inside the heads of the test question writers to help you understand and outsmart the GMAT question mentality.
Dedicated preparation with Nova’s GMAT Prep Course has been shown to significantly increase GMAT scores. If you want to get your best score on the GMAT, you can’t afford not to try it!
Features:
- Math: Twenty-two chapters provide comprehensive review of GMAT math.
- Logical Reasoning: Discover the underlying simplicity of these problems and learn the tactics the GMAT writers use to obfuscate the answers.
- Reading Comprehension: Develop the ability to spot places from which questions are likely to be drawn as you read a GMAT passage (pivotal words, counter-premises, etc.).
- Mentor Exercises: These exercises provide hints, insight, and partial solutions to ease your transition from seeing GMAT problems solved to solving them on your own.
- Test Mentality: 15% of this book is dedicated to training you to think like a test writer to help you spot red herrings AND correct answers.
- Hundreds of GMAT-style questions with detailed solutions!
- Study plan suggestions based on the amount of time you have before the exam
Testimonials:
“Far and away the best book…After doing all drills in Nova, the commonly considered difficult practice questions in Kaplan were almost a joke. I would recommend to anyone this book.”
“I got a 690 on the GMAT using only this book, and studying sporadically for a few weeks leading up to the test.”
“I am very happy to say that at the GMAT exam, for which I studied with this book, I received 710 points.”
“I am a Professor of English, and… I make it my business to find books and use them to help students get into graduate school. I have found the Nova book complete in every aspect… Without unnecessary rhetoric, the text is exact, with comprehensive yet concise answers, in the math and verbal sections. This is definitely a three year crash course in a several month program.”
Pages 602
Price: $23.97
ISBN: 1889057401
Purchase GMAT Prep Course (Domestic) (printed book) (Free shipping within the United States.) (We do not ship outside of the United States.)
SUBSTITUTION
Substitution is a very useful technique for solving GMAT math problems. It often reduces hard problems to routine ones. In the substitution method, we choose numbers that have the properties given in the problem and plug them into the answer-choices.
Example: If n is an odd integer, which one of the following is an even integer?
(A) 3n + 2
(B) n/4
(C) 2n + 3
(D) n(n + 3)
(E) nn
We are told that n is an odd integer. So choose an odd integer for n, say, 1 and substitute it into each answer-choice. In Choice (A), 3(1) + 2 = 5, which is not an even integer. So eliminate (A). Next, n/4 = 1/4 is not an even integer–eliminate (B). Next, 2n + 3 = 2(1) + 3 = 5 is not an even integer–eliminate (C). Next, n(n + 3) = 1(1 + 3) = 4 is even and hence the answer is possibly (D). Finally, in Choice (E), nn = 1(1) = 1, which is not even–eliminate (E). The answer is (D).
When using the substitution method, be sure to check every answer-choice because the number you choose may work for more than one answer-choice. If this does occur, then choose another number and plug it in, and so on, until you have eliminated all but the answer. This may sound like a lot of computing, but the calculations can usually be done in a few seconds.
When using the substitution method, be sure to check every answer-choice because the number you choose may work for more than one answer-choice. If this does occur, then choose another number and plug it in, and so on, until you have eliminated all but the answer. This may sound like a lot of computing, but the calculations can usually be done in a few seconds.
Example : If n is an integer, which of the following CANNOT be an even integer?
(A) 2n + 2
(B) n – 5
(C) 2n
(D) 2n + 3
(E) 5n +2
Choose n to be 1. Then 2n + 2 = 2(1) + 2 = 4, which is even. So eliminate (A). Next, n – 5 = 1 – 5 = -4. Eliminate (B). Next, 2n = 2(1) = 2. Eliminate (C). Next, 2n + 3 = 2(1) + 3 = 5 is not even–it may be our answer. However, 5n + 2 = 5(1) + 2 = 7 is not even as well. So we choose another number, say, 2. Then 5n + 2 = 5(2) + 2 = 12 is even, which eliminates (E). Thus, choice (D), 2n + 3, is the answer.
DEFINED FUNCTIONS
Defined functions are very common on the GMAT, and most students struggle with them. Yet once you get used to them, defined functions can be some of the easiest problems on the GMAT. In this type of problem, you will be given a symbol and a property that defines the symbol.
Example: Define x # y by the equation x # y = xy – y. Then 2 # 3 =
(A) 1
(B) 3
(C) 12
(D) 15
(E) 18
From the above definition, we know that x # y = xy – y. So all we have to do is replace x with 2 and y with 3 in the definition: 2 # 3 = 2(3) – 3 = 3. Hence, the answer is (B).
NUMBER THEORY
This broad category is a popular source for GMAT questions. At first, students often struggle with these problems since they have forgotten many of the basic properties of arithmetic. So before we begin solving these problems, let’s review some of these basic properties.
“The remainder is r when p is divided by q” means p = qz + r; the integer z is called the quotient. For instance, “The remainder is 1 when 7 is divided by 3” means 7 = 3(2) + 1.
Example: When the integer n is divided by 2, the quotient is u and the remainder is 1. When the integer n is divided by 5, the quotient is v and the remainder is 3. Which one of the following must be true?
(A) 2u + 5v = 4
(B) 2u – 5v = 2
(C) 4u + 5v = 2
(D) 4u – 5v = 2
(E) 3u – 5v = 2
Translating “When the integer n is divided by 2, the quotient is u and the remainder is 1” into an equation gives n = 2 u + 1. Translating “When the integer n is divided by 5, the quotient is v and the remainder is 3” into an equation gives n = 5v + 3. Since both expressions equal n, we can set them equal to each other: 2u + 1 = 5v + 3. Rearranging and then combining like terms yields 2u – 5v = 2. The answer is (B).
- A number n is even if the remainder is zero when n is divided by 2: n = 2z + 0, or n = 2z.
- A number n is odd if the remainder is one when n is divided by 2: n = 2z + 1.
- The following properties for odd and even numbers are very useful–you should memorize them:
even x even = even
odd x odd = odd
even x odd = even
even + even = even
odd + odd = even
even + odd = odd
- Consecutive integers are written as x, x + 1, x + 2, . . .
- Consecutive even or odd integers are written as , x + 2, x + 4, . . .
- The integer zero is neither positive nor negative, but it is even: 0 = 2(0).
- A prime number is an integer that is divisible only by itself and 1.The prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, . . .
- A number is divisible by 3 if the sum of its digits is divisible by 3.For example, 135 is divisible by 3 because the sum of its digits (1 + 3 + 5 = 9) is divisible by 3.
- The absolute value of a number, | |, is always positive. In other words, the absolute value symbol eliminates negative signs.
For example, | -7 | = 7. Caution, the absolute value symbol acts only on what is inside the symbol, | |. For example, -| -7 | = -(+7) = -7. Here, only the negative sign inside the absolute value symbol is eliminated.
Example: If a, b, and c are consecutive integers and a < b < c, which of the following must be true?
I. b – c = 1
II. abc/3 is an integer.
III. a + b + c is even.
(A) I only (B) II only (C) III only (D) I and II only (E) II and III only
Let x, x + 1, x + 2 stand for the consecutive integers a, b, and c, in that order. Plugging this into Statement I yields b – c = (x + 1) – (x + 2) = -1. Hence, Statement I is false.
As to Statement II, since a, b, and c are three consecutive integers, one of them must be divisible by 3. Hence, abc/3 is an integer, and Statement II is true.
As to Statement III, suppose a is even, b is odd, and c is even. Then a + b is odd since even + odd = odd. Hence, a + b + c = (a + b) + c = (odd) + even = odd. Thus, Statement III is not necessarily true. The answer is (B).
GEOMETRY
One-fourth of the math problems on the GMAT involve geometry. (There are no proofs.) Fortunately, except for Data Sufficiency section, the figures on the GMAT are usually drawn to scale. Hence, you can check your work and in some cases even solve a problem by “eyeballing” the drawing.
Following are some of the basic properties of geometry. You probably know many of them. Memorize any that you do not know.
1. There are 180 degrees in a straight angle.
2. Two angles are supplementary if their angle sum is 180 degrees.
3. Two angles are complementary if their angle sum is 90 degrees.
4. Perpendicular lines meet at right angles.
5. A triangle with two equal sides is called isosceles. The angles opposite the equal sides are called the base angles.
6. The altitude to the base of an isosceles or equilateral triangle bisects the base and bisects the vertex angle.
7. The angle sum of a triangle is 180 degrees.
8. In an equilateral triangle all three sides are equal, and each angle is 60 degrees.
9. The area of a triangle is bh/2, where b is the base and h is the height.
10. In a triangle, the longer side is opposite the larger angle, and vice versa.
11. Two triangles are similar (same shape and usually different size) if their corresponding angles are equal. If two triangles are similar, their corresponding sides are proportional.
12. Two triangles are congruent (identical) if they have the same size and shape.
13. In a triangle, an exterior angle is equal to the sum of its remote interior angles and is therefore greater than either of them.
14. Opposite sides of a parallelogram are both parallel and congruent.
15. The diagonals of a parallelogram bisect each other.
16. If w is the width and l is the length of a rectangle, then its area is A = lw and its perimeter is P = 2w + 2l.
17. The volume of a rectangular solid (a box) is the product of the length, width, and height. The surface area is the sum of the area of the six faces.
18. If the length, width, and height of a rectangular solid (a box) are the same, it is a cube. Its volume is the cube of one of its sides, and its surface area is the sum of the areas of the six faces.
19. A tangent line to a circle intersects the circle at only one point. The radius of the circle is perpendicular to the tangent line at the point of tangency.
20. An angle inscribed in a semicircle is a right angle.
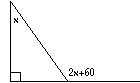
Example: In the figure above, what is the value of x?
(A) 30
(B) 32
(C) 35
(D) 40
(E) 47
Since 2x + 60 is an exterior angle, it is equal to the sum of the remote interior angles. That is, 2x + 60 = x + 90. Solving for x gives x = 30. The answer is (A).
Most geometry problems on the GMAT require straightforward calculations. However, some problems measure your insight into the basic rules of geometry. For this type of problem, you should step back and take a “birds-eye” view of the problem. The following example will illustrate.
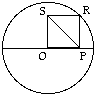
Example: In the figure above, O is both the center of the circle with radius 2 and a vertex of the square OPRS. What is the length of diagonal PS?
(A) 1/2
(B) 1
(C) 4
(D) 2
(E) 2/3
The diagonals of a square are equal. Hence, line segment OR (not shown) is equal to SP. Now, OR is a radius of the circle and therefore OR = 2. Hence, SP = 2 as well, and the answer is (D).
INEQUALITIES
Inequalities are manipulated algebraically the same way as equations with one exception:
Multiplying or dividing both sides of an inequality by a negative number reverses the inequality. That is, if x > y and c < 0, then cx < cy.
Example: For which values of x is 4x + 3 > 6x – 8?
As with equations, our goal is to isolate x on one side:
Subtracting 6x from both sides yields -2x + 3 > -8.
Subtracting 3 from both sides yields -2x > -11.
Dividing both sides by -2 and reversing the inequality yields x < 11/2.
Positive & Negative Numbers
A number greater than 0 is positive. On the number line, positive numbers are to the right of 0. A number less than 0 is negative. On the number line, negative numbers are to the left of 0. Zero is the only number that is neither positive nor negative; it divides the two sets of numbers. On the number line, numbers increase to the right and decrease to the left.
The expression x > y means that x is greater than y. In other words, x is to the right of y on the number line.
We usually have no trouble determining which of two numbers is larger when both are positive or one is positive and the other negative (e.g., 5 > 2 and 3.1 > -2). However, we sometimes hesitate when both numbers are negative (e.g., -2 > -4.5). When in doubt, think of the number line: if one number is to the right of the number, then it is larger.
Absolute Value
The absolute value of a number is its distance on the number line from 0. Since distance is a positive number, absolute value of a number is positive. Two vertical bars denote the absolute value of a number: | x |. For example, | 3 | = 3 and | -3 | = 3.
Students rarely struggle with the absolute value of numbers: if the number is negative, simply make it positive; and if it is already positive, leave it as is. For example, since -2.4 is negative, | -2.4 | = 2.4 and since 5.01 is positive | 5.01 | = 5.01.
Further, students rarely struggle with the absolute value of positive variables: if the variable is positive, simply drop the absolute value symbol. For example, if x > 0, then | x | = x.
However, negative variables can cause students much consternation. If x is negative, then | x | = -x. This often confuses students because the absolute value is positive but the -x appears to be negative. It is actually positive–it is the negative of a negative number, which is positive. To see this more clearly let x = -k, where k is a positive number. Then x is a negative number. So | x | = -x = -(-k) = k. Since k is positive so is -x. Another way to view this is | x | = -x = (-1)x = (-1)(a negative number) = a positive number.
Transitive Property
If x < y and y < z, then x < z.
Example: If 1/Q > 1, is 1 > QQ ?
Since 1/Q > 1 and 1 > 0, we know from the transitive property that 1/Q is positive. Hence, Q is positive. Therefore, we can multiply both sides of 1/Q > 1 by Q without reversing the inequality:
Q(1/Q) > 1(Q) Reducing yields 1 > Q Multiplying both sides again by Q yields Q > QQ Using the transitive property to combine the last two inequalities yields 1 > QQ
FRACTIONS
I. To compare two fractions, cross-multiply. The larger number will be on the same side as the larger fraction.
Example: Example: Which fraction is greater 9/10 or 10/11 ?
Cross-multiplying gives (9)(11) versus (10)(10), which reduces to 99 versus 100. Now, 100 is greater than 99. Hence, 10/11 is greater than 9/10.
III. To solve a fractional equation, multiply both sides by the LCD (lowest common denominator) to clear fractions.
Example: If (x + 3)/(x – 3) = y, what is the value of x in terms of y?
(A) 3 – y
(B) 3/y
(C) (2 + y)/(y – 2)
(D) (-3y -3)/(1 – y)
(E) 3y/2
First, multiply both sides of the equation by x – 3: (x – 3)(x + 3)/(x – 3) = (x – 3)y
Cancel the (x – 3’s) on the left side of the equation: x + 3 = (x – 3)y
Distribute the y: x + 3 = xy – 3y
Subtract xy and 3 from both sides: x – xy = -3y – 3
Factor out the x on the left side of the equation: x(1 – y) = -3y – 3
Finally, divide both sides of the equation by 1 – y: x = (-3y -3)/(1 – y)
Hence, the answer is (D).
IV. When dividing a fraction by a whole number (or vice versa), you must keep track of the main division bar.
Example: a/(b/c) = a(c/b) = ac/b. But (a/b)/c = (a/b)(1/c) = a/(bc).
V. Two fractions can be added quickly by cross-multiplying:
a/b + c/d = (ad + bc)/bd
Example: 1/2 – 3/4 =
(A) -5/4
(B) -2/3
(C) -1/4
(D) 1/2
(E) 2/3
Cross multiplying the expression 1/2 – 3/4 yields [1(4) – 2(3)]/2(4) = (4 – 6)/8 = -2/8 = -1/4. Hence, the answer is (C).
AVERAGES
Problems involving averages are very common on the GMAT. They can be classified into four major categories as follows.
I. The average of N numbers is their sum divided by N, that is, average = sum/N.
Example: The average of x, 2x, and 6 is (x + 2x + 6)/3 = (3x + 6)/3 = 3(x + 2)/3 = x + 2.
II. Weighted average: The average between two sets of numbers is closer to the set with more numbers.
Example: If on a test three people answered 90% of the questions correctly and two people answered 80% correctly, then the average for the group is not 85% but rather [3(90) + 2(80)]/5 = 430/5 = 86. Here, 90 has a weight of 3–it occurs 3 times. Whereas 80 has a weight of 2–it occurs 2 times. So the average is closer to 90 than to 80 as we have just calculated.
III. Using an average to find a number.
Sometimes you will be asked to find a number by using a given average. An example will illustrate.
Example: If the average of five numbers is -10, and the sum of three of the numbers is 16, then what is the average of the other two numbers?
(A) -33
(B) -1
(C) 5
(D) 20
(E) 25
Let the five numbers be a, b, c, d, e. Then their average is (a + b + c + d + e)/5 = -10. Now three of the numbers have a sum of 16, say, a + b + c = 16. So substitute 16 for a + b + c in the average above: (16 + d + e)/5 = -10. Solving this equation for d + e gives d + e = -66. Finally, dividing by 2 (to form the average) gives (d + e)/2 = -33. Hence, the answer is (A).
RATIO & PROPORTION
Ratio
A ratio is simply a fraction. Both of the following notations express the ratio of x to y: x:y, x/y. A ratio compares two numbers. Just as you cannot compare apples and oranges, so too must the numbers you are comparing have the same units. For example, you cannot form the ratio of 2 feet to 4 yards because the two numbers are expressed in different units–feet vs. yards. It is quite common for the GMAT to ask for the ratio of two numbers with different units. Before you form any ratio, make sure the two numbers are expressed in the same units.
Proportion
A proportion is simply an equality between two ratios (fractions). For example, the ratio of x to y is equal to the ratio of 3 to 2 is translated as x/y = 3/2. Two variables are directly proportional if one is a constant multiple of the other:
y = kx, where k is a constant.
The above equation shows that as x increases (or decreases) so does y. This simple concept has numerous applications in mathematics. For example, in constant velocity problems, distance is directly proportional to time: d = vt, where v is a constant. Note, sometimes the word directly is suppressed.
Example: If the ratio of y to x is equal to 3 and the sum of y and x is 80, what is the value of y?
(A) -10
(B) -2
(C) 5
(D) 20
(E) 60
Translating “the ratio of y to x is equal to 3” into an equation yields: y/x = 3
Translating “the sum of y and x is 80” into an equation yields: y + x = 80
Solving the first equation for y gives: y = 3x.
Substituting this into the second equation yields
3x + x = 80
4x = 80
x = 20
Hence, y = 3x = 3(20) = 60. The answer is (E).
EXPONENTS & ROOTS
Exponents
There are five rules that govern the behavior of exponents:
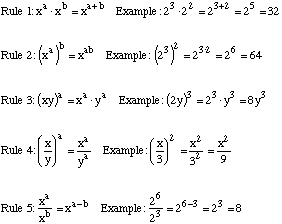
Problems involving these five rules are common on the GMAT, and they are often listed as hard problems. However, the process of solving these problems is quite mechanical: simply apply the five rules until they can no longer be applied.
Roots
There are only two rules for roots that you need to know for the GMAT:
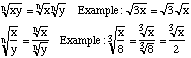
FACTORING
To factor an algebraic expression is to rewrite it as a product of two or more expressions, called factors. In general, any expression on the GMAT that can be factored should be factored, and any expression that can be unfactored (multiplied out) should be unfactored.
Distributive Rule
The most basic type of factoring involves the distributive rule:
ax + ay = a(x + y)
For example, 3h + 3k = 3(h + k), and 5xy + 45x = 5xy + 9(5x) = 5x(y + 9). The distributive rule can be generalized to any number of terms. For three terms, it looks like ax + ay + az = a(x + y + z). For example, 2x + 4y + 8 = 2x + 2(2y) + 2(4) = 2(x + 2y + 4).
Example: If x – y = 9, then (x – y/3) – (y – x/3) =
(A) -4
(B) -3
(C) 0
(D) 12
(E) 27
(x – y/3) – (y – x/3) =
x – y/3 – y + x/3 =
4x/3 – 4y/3 =
4(x – y)/3 =
4(9)/3 =
12
The answer is (D).
Difference of Squares
One of the most important formulas on the GMAT is the difference of squares:
![]()
Example: If x does not equal -2, then![]()
(A) 2(x – 2)
(B) 2(x – 4)
(C) 8(x + 2)
(D) x – 2
(E) x + 4
In most algebraic expressions involving multiplication or division, you won’t actually multiply or divide, rather you will factor and cancel, as in this problem.
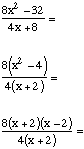
2(x – 2)
The answer is (A).
ALGEBRAIC EXPRESSIONS
A mathematical expression that contains a variable is called an algebraic expression. Some examples of algebraic expressions are 3x – 2y, 2z/y. Two algebraic expressions are called like terms if both the variable parts and the exponents are identical. That is, the only parts of the expressions that can differ are the coefficients. For example, x + y and -7(x + y) are like terms. However, x – y and 2 – y are not like terms.
Adding & Subtracting Algebraic Expressions
Only like terms may be added or subtracted. To add or subtract like terms, merely add or subtract their coefficients:
![]()
You may add or multiply algebraic expressions in any order. This is called the commutative property:
x + y = y + x xy = yx
For example, -2x + 5x = 5x + (-2x) = (5 – 2)x = -3x and (x – y)(-3) = (-3)(x – y) = (-3)x – (-3)y = -3x + 3y.
Caution: the commutative property does not apply to division or subtraction.
When adding or multiplying algebraic expressions, you may regroup the terms. This is called the associative property:
x + (y + z) = (x + y) + z x(yz) = (xy)z
Notice in these formulas that the variables have not been moved, only the way they are grouped has changed: on the left side of the formulas the last two variables are grouped together, and on the right side of the formulas the first two variables are grouped together.
For example, (x -2x) + 5x = (x + [-2x]) + 5x = x + (-2x + 5x) = x + 3x = 4x and 24x = 2x(12x) = 2x(3x4x) = (2x3x)4x = 6x4x = 24x
Caution: the associative property doesn’t apply to division or subtraction.
Notice in the first example that we changed the subtraction into negative addition: (x – 2x) = (x + [- 2x]). This allowed us to apply the associative property over addition.
Order of Operations: (PEMDAS)
When simplifying algebraic expressions, perform operations within parentheses first and then exponents and then multiplication and then division and then addition and then subtraction. This can be remembered by the mnemonic:
PEMDAS Please Excuse My Dear Aunt Sally
GRAPHS
Questions involving graphs rarely involve any significant calculating. Usually, the solution is merely a matter of interpreting the graph.

1. During which year was the company’s earnings 10 percent of its sales?
(A) 85
(B) 86
(C) 87
(D) 88
(E) 90
Reading from the graph, we see that in 1985 the company’s earnings were $8 million and its sales were $80 million. This gives 8/80 = 1/10 = 10/100 = 10%. The answer is (A).
2. During what two-year period did the company’s earnings increase the greatest?
(A) 85-87
(B) 86-87
(C) 86-88
(D) 87-89
(E) 88-90
Reading from the graph, we see that the company’s earnings increased from $5 million in 1986 to $10 million in 1987, and then to $12 million in 1988. The two-year increase from ’86 to ’88 was $7 million–clearly the largest on the graph. The answer is (C).
3. During the years 1986 through 1988, what were the average earnings per year?
(A) 6 million
(B) 7.5 million
(C) 9 million
(D) 10 million
(E) 27 million
The graph yields the following information:
| Year | Earnings |
| 1986 | $5 million |
| 1987 | $10 million |
| 1988 | $12 million |
Forming the average yields (5 + 10 + 12)/3 = 27/3 = 9. The answer is (C).
4. If Consolidated Conglomerate’s earnings are less than or equal to 10 percent of sales during a year, then the stockholders must take a dividend cut at the end of the year. In how many years did the stockholders of Consolidated Conglomerate suffer a dividend cut?
(A) None
(B) One
(C) Two
(D) Three
(E) Four
Calculating 10 percent of the sales for each year yields
| Year | 10% of Sales (millions) | Earnings (millions) |
| 85 | .10 x 80 = 8 | 8 |
| 86 | .10 x 70 = 7 | 5 |
| 87 | .10 x 50 = 5 | 10 |
| 88 | 10 x 80 = 8 | 12 |
| 89 | .10 x 90 = 9 | 11 |
| 90 | .10 x 100 = 10 | 8 |
Comparing the right columns shows that earnings were 10 percent or less of sales in 1985, 1986, and 1990. The answer is (D).
WORD PROBLEMS
Although exact steps for solving word problems cannot be given, the following guidelines will help:
1) First, choose a variable to stand for the least unknown quantity, and then try to write the other unknown quantities in terms of that variable.
For example, suppose we are given that Sue’s age is 5 years less than twice Jane’s and the sum of their ages is 16. Then Jane’s age would be the least unknown, and we let x = Jane’s age. Expressing Sue’s age in terms of x gives Sue’s age = 2x – 5.
2) Second, write an equation that involves the expressions in Step 1. Most (though not all) word problems pivot on the fact that two quantities in the problem are equal. Deciding which two quantities should be set equal is usually the hardest part in solving a word problem since it can require considerable ingenuity to discover which expressions are equal.
For the example above, we would get (2x – 5) + x = 16.
3) Third, solve the equation in Step 2 and interpret the result.
For the example above, we would get by adding the x’s: 3x – 5 = 16. Then adding 5 to both sides gives 3x = 21. Finally, dividing by 3 gives x = 7. Hence, Jane is 7 years old and Sue is 2x – 5 = 2(7) – 5 = 9 years old.
Motion Problems
Virtually, all motion problems involve the formula Distance = Rate x Time, or
D = R x T
Example : Scott starts jogging from point X to point Y. A half-hour later his friend Garrett who jogs 1 mile per hour slower than twice Scott’s rate starts from the same point and follows the same path. If Garrett overtakes Scott in 2 hours, how many miles will Garrett have covered?
(A) 2 1/5
(B) 3 1/3
(C) 4
(D) 6
(E) 6 2/3
Following Guideline 1, we let r = Scott’s rate. Then 2r – 1 = Garrett’s rate. Turning to Guideline 2, we look for two quantities that are equal to each other. When Garrett overtakes Scott, they will have traveled the same distance. Now, from the formula D = R x T, Scott’s distance is D = r x 2 1/2 and Garrett’s distance is D = (2r – 1)2 = 4r – 2. Setting these expressions equal to each other gives 4r – 2 = r x 2 1/2. Solving this equation for r gives r = 4/3. Hence, Garrett will have traveled D = 4r – 2 = 4(4/3) – 2 = 3 1/3 miles. The answer is (B).
Work Problems
The formula for work problems is Work = Rate x Time, or W = R x T. The amount of work done is usually 1 unit. Hence, the formula becomes 1 = R x T. Solving this for R gives R = 1/T.
Example : If Johnny can mow the lawn in 30 minutes and with the help of his brother, Bobby, they can mow the lawn 20 minutes, how long would take Bobby working alone to mow the lawn?
(A) 1/2 hour
(B) 3/4 hour
(C) 1 hour
(D) 3/2 hours
(E) 2 hours
Let r = 1/t be Bobby’s rate. Now, the rate at which they work together is merely the sum of their rates:
Total Rate = Johnny’s Rate + Bobby’s Rate
1/20 = 1/30 + 1/t
1/20 – 1/30 = 1/t
(30 – 20)/(30)(20) = 1/t
1/60 = 1/t
t = 60
Hence, working alone, Bobby can do the job in 1 hour. The answer is (C).



